概述

本篇属于理论篇，介绍了针对二元分类问题的 Logistic 回归与梯度下降，以及 Logistic 回归当中的梯度下降是如何进行参数优化的。

Title

1.0 Logistic 回归概述

Logistic 回归是一种广义上的线性回归，也是一个用在监督学习当中的学习算法，一般用于输出值为0或1，即"是"或"不是"的问题当中，这就是二元分类问题。

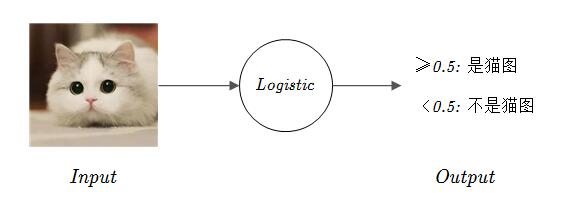
例如给定一个 $x$ ，假设这个 $x$ 是一张图片，你想要识别它是不是一张猫的图片，如果是猫的图片就输出1，如果不是就输出0，那么这就是一个典型的二元分类问题，你需要一个算法使得对于输入 $x$ ，能够得出一个预测值 $\hat{y}$ ，或者说对于二元分类问题而言， $\hat{y}$ 需要是一个概率值，位于区间 $[0,1]$ 当中，代表分类的倾向。

就拿猫图识别来说，如果输入一张图片得到的输出 $\hat{y}=0.83$ 的话，由于这个概率大于 50%，因此你可以认为它有可能是一张猫图。

识别是不是猫图是一个二元分类问题

图1-1 识别是不是猫图是一个二元分类问题

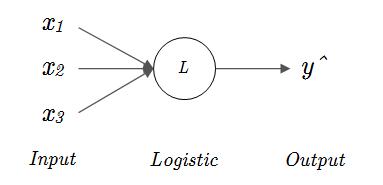
假设你有一个需要预测的内容，要通过三个输入， $x_1$ 、 $x_2$ 和 $x_3$ 的某种线性组合来预测某个问题，或者说知道某件事情发生的概率 $z$ 的话，那么用 logistic 回归来表达就是

\\begin{equation} z = w_1x_1 + w_2x_2 + w_3x_3 + b \\end{equation}

但是为了简洁与方便计算，一般单样本的输入与参数都写作列矩阵的形式，第 $i$ 个样本的各项输入用矩阵 $x^{(i)}$ 来表示，各项输入的系数用矩阵 $w$ 来表示。例如对于第 $i$ 个样本 $x$ 而言它有 $n_x$ 个输入，那么它就对应一个 $n_x \times 1$ 的列矩阵 $x^{(i)}$ ，这样就得到了 Logistic 回归的矩阵形式，也是你常见到的形式：

\\begin{equation} z^{(i)} = w^Tx^{(i)} + b \\end{equation}

公式(2)表示的是单个样本的计算，在大多数情况下我们会将许多样本按行堆叠在一起，放在一个更大的矩阵当中，并用相应的大写字母来表示这个数据的样本集合，例如对于一个有 $n_x$ 个输入， $m$ 个样本的训练集合来说，一般使用大写字母 $X$ 来表示：

\begin{equation} X = \begin{bmatrix} {\vdots}&{\vdots}&{\vdots}&{\vdots}\\\\ x^{(1)}&x^{(2)}&{\cdots}&x^{(m)}\\\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\\\ \end{bmatrix} \_{n_x \times m} , w = \begin{bmatrix} w_1\\\\ w_2\\\\ {\vdots}\\\\ w_{n_x}\\\\ \end{bmatrix} \_{n_x \\times 1} \end{equation}

如果你学过线性代数的话也许能够理解上面公式的意义，这种表示形式更像是一种技术，使用这种表示形式在深度学习当中是非常重要的，它能够在很大程度上提高我们模型的训练效率。

如果你不理解我所说的话也不用着急，在第二篇当中你将详细地认识这门技术，并且为其精妙而感叹。在本篇当中我们只考虑单个样本的情况，因此你可以选择暂时忽略公式(3)。例如对于这个三个输入问题的单个样本而言， $x$ 与 $w$ 就分别是下面这样的 $3 \times 1$ 矩阵：

\begin{equation} x = \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix} , w = \begin{bmatrix} w_1\\ w_2\\ w_3\\ \end{bmatrix} \end{equation}

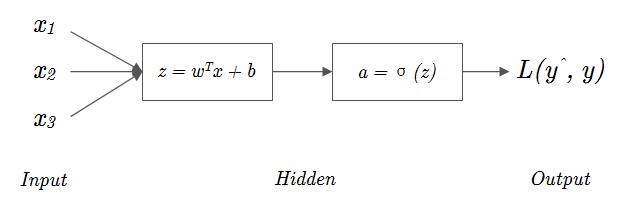
用图像可以将这个单样本的 Logistic 回归过程更加直观地表示出来，其中 $\hat{y}$ 就是输出值 $z$ 。

Logistic 回归过程

图1-2 Logistic 回归过程

1.1 sigmoid 激活函数

在前面你已经了解了什么是二元分类问题，知道了 Logistic 回归是一种可以用于处理二元分类问题的学习算法，但是如果真正要做二元分类，你会发现 Logistic 回归的输出值 $z$ ，是关于输入层 $x$ 的线性组合，所以 $z$ 的数值范围是不确定的。你更希望得到一个介于0和1之间的概率值，而不是一个可能大到非常大，小可以小到很小的不确定的数字。Sigmoid 函数就可以帮助你将输入 $z$ 转换到区间 $[0,1]$ 上，使你可以根据输入 $x$ 得到的输出概率更好进行分类。Sigmoid 函数表达式与其在 $[-10,10]$ 上的图像见公式(5) 与图1-3：

\begin{equation} \sigma(z) = \frac{1}{1+e^{-z}} \end{equation}

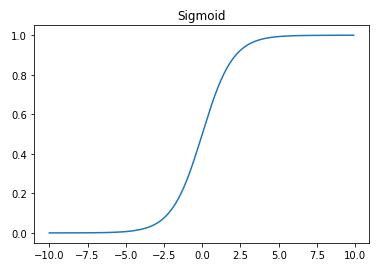
sigmoid 函数图形

图1-3 sigmoid 函数图形

当 $z$ 越来越小时， $e^{-z}$ 就会越来越大，对应的表达式的分母就会越来越大，使得 $\sigma(z)$ 逐渐趋于0；
当 $z$ 越来越大时， $e^{-z}$ 就会越来越小并趋近于0，对应的表达式的分母就会越来越趋近于1，使得 $\sigma(z)$ 逐渐趋于1。

这样，通过 $\sigma(z)$ 函数的转换和帮助，你可以用 Logistic 回归来得到一个概率输出了。一般我们将 Logistic 的计算结果用小写字母 $z$ 来表示，而通过 $\sigma(z)$ 函数映射后得到的最终概率输出，用小写字母 $a$ 来表示。

现在，我们可以得到改造后的 Logistic 二元分类回归过程了（图1-4）

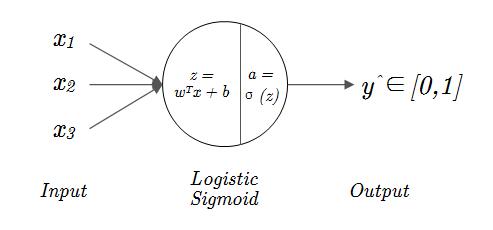
二元分类问题的 Logistic 回归

图1-4 二元分类问题的 Logistic 回归

你可能有注意到，图1-4 当中的 Output 并不是写的 $a$ ，而是 $\hat{y}$ ，这是为了将最终输出与隐藏层当中的量区分开来。

如果你不知道什么是隐层的话，图1-4 中间的圆圈（Logistic/Sigmoid），在神经网络当中就被称作隐层(Hidden layer)，也被叫做隐藏层。

之所以要这么叫它，是因为通常我们只在意输入的数据通过隐层后得到了怎样的输出，而并不在意其中的数值以及在内部所做的计算，在神经网络运行的过程当中我们也无法看到其中的细节，因此将其称作隐层。

你可能不会相信，这就是一个简单的神经网络了，只不过它只有一个隐藏层，看上去非常的简单简洁。这样只有一个隐层的神经网络又被称作单层神经网络(Single-layer neural network)（输入层与输出层是不计入神经网络的层数的），在今后我们会看到更加复杂的网络。

1.2 Logistic 回归损失函数

Loss Function

在前面你已经认识了 sigmoid 函数，知道了借助于 sigmoid 函数我们可以将 Logistic 回归的计算结果映射到区间 $[0,1]$ 上以表示一个概率。至此，我们已经可以通过 Logistic 回归得到关于输入 $x$ 的一个预测输出 $\hat{y}$ 了。接下来想一想，我们需要怎样来衡量这个预测值 $\hat{y}$ 的准确度？我猜你一定想到了一种常用的度量方法，那就是距离(Distance)。

在很多情况下，我们使用距离公式来衡量两个量之间的差距，对于 Logistic 回归而言，如果关于 $x$ 的正确输出是 $y$ 的话，那么使用距离来衡量预测差距的公式就是：

\begin{equation} D(\hat{y},y) = (\hat{y}-y)^2 \end{equation}

这个公式看上去非常的简洁，但是在神经网络，或者说在深度学习当中，我们不会选用这个函数，而是使用另一个名为**损失函数(Loss function)**的函数来衡量，这个函数的表达式是这样的：

\begin{equation} L(\hat{y},y) = -[ ylog(\hat{y}) + (1-y)log(1-\hat{y}) ] \end{equation}

我们先来看一看这个看上去很复杂的 Loss Function 能否起到衡量输出准确的作用，为了使得输出尽可能准确，我们要做的就是使得损失函数尽可能小：

当正确输出 $y=0$ 时，表达式变成了公式(8)，为了使得 $L(\hat{y},y)$ 尽可能小， $log(1-\hat{y})$ 就要尽可能大，也就是 $1-\hat{y}$ 要尽可能大，最终结果是 $\hat{y}$ 要尽可能小，而 $\hat{y} \in [0,1]$ ，因此 $\hat{y}$ 需要尽可能接近于0，也就是正确输出 $y$ 。

\begin{equation} L(\hat{y},y) = -log(1-\hat{y}) \end{equation}

当正确输出 $y=1$ 时，表达式变成了公式(9)，为了使得 $L(\hat{y},y)$ 尽可能小， $log(\hat{y})$ 就要尽可能大，最终结果是 $\hat{y}$ 要尽可能大，而 $\hat{y} \in [0,1]$ ，因此 $\hat{y}$ 需要尽可能接近于1，也就是正确输出 $y$ 。

\begin{equation} L(\hat{y},y) = -log(\hat{y}) \end{equation}

看来，通过 Loss Function 我们确实可以使得 $\hat{y}$ 与 $y$ 向同一趋势靠近，可是为什么有简单的距离函数不用，却要用这个看上去更复杂的损失函数呢？

这是因为如果使用距离函数 $D(\hat{y},y)$ ，那么对应的 Cost 函数 $J(w,b)$ 将是非凸的，这会产生许多的局部最小值，导致在梯度下降的过程当中难以找到全局最优解。而损失函数是凸的，这就有利于我们在后面进行梯度下降。如果你看不懂上面这段话也不用担心，因为在后面你将会明白其中的原因。

至此，你已经完成了 Logsitic 回归单层神经网络的一半内容，对于 Logistic 回归来说，我们在1.1节的图1-4 中已经看过他的计算流程了，这一从输入 $x$ 到完成 $L(\hat{y},y)$ 计算的过程被称作向前传播(Forward-propagation)，图1-5 给出的就是这个过程。

Logistic 回归的向前传播过程

图1-5 Logistic 回归的向前传播过程

Cost Function

在前面你已见过了损失函数 Loss Function，并且知道了通过 Loss Function 可以了解 Logistic 回归的预测输出 $\hat{y}$ 相对于正确输出的偏差程度。现在你将见到 Cost Funtion，这个函数同样也可以叫做损失函数，不过它和 Loss Function 有些不同，一般称其为成本函数(Cost Function)，我们来看一看。

相信你已经发现了，Loss Funtion 的输入参数是， $\hat{y}$ 和 $y$ ，这说明了 Loss Function 是用于衡量单个样本的预测输出与正确输出的差距的。相信你之前了解过，深度学习需要巨大的数据集进行神经网络的训练，可是，单个样本的损失函数不能代表整体，一个样本预测的准确，不能代表在整个数据集上表现良好。

因此 Cost Funtion 就是用来衡量参数 $w$ 和 $b$ 对所有样本的适应情况的，这样你应该能够很好的理解，Cost Funtion 就是的对所有样本 Loss Funtion 的均值：

\begin{equation} J(w,b) = \frac{1}{m}\sum_{i=1}^m L(\hat{y},y) = -\frac{1}{m}\sum_{i=1}^m [ ylog(\hat{y}) + (1-y)log(1-\hat{y}) ] \end{equation}

正如你看到的，Cost Funtion 一般用 $J(w,b)$ 来表示，这应该不难理解，Cost Funtion 就是用来衡量 $w$ 、 $b$ 两个参数的全局表现的。

当w、b是实数时，J(w,b)函数的图形

图1-6 当 $w$、$b$ 是实数时，$J(w,b)$ 函数的图像

1.3 梯度下降法

在前面你已经完成了 Logistic 回归的向前传播，认识了损失函数 Loss Function 和 Cost Funtion，它们中的前一个是衡量我们的神经网络模型对单个样本的预测情况，后一个是前一个在数据集上的均值，衡量我们的神经网络模型在整个数据集上的表现。下面，我们可以开始看看怎样调节参数 $w$ 和 $b$ ，来优化我们的神经网络了。

为了使得模型的效果更好，我们需要着眼的是怎样调节 $w$ 和 $b$ ，使得 Cost Function $J(w,b)$ 尽可能小。

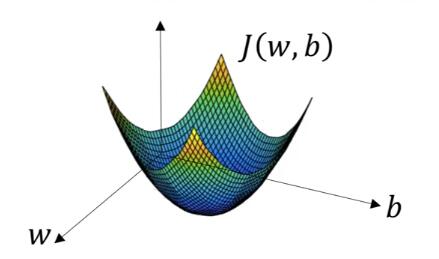
在图1-6 中你看到了当 $w$ 和 $b$ 是实数情况下的 $J(w,b)$ 函数图像，为了方便起见，我们暂时忽略 $b$ ，只看 $w$ 对 $J(w)$ 的影响，你将在图1-7 看到它的形态。

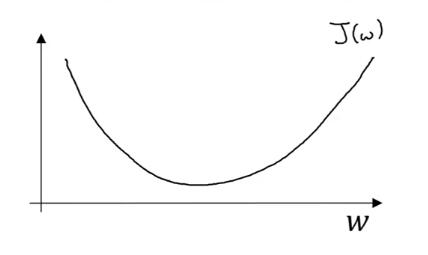
当w是实数时，J(w)函数的图形

图1-7 当 $w$ 是实数时，$J(w)$ 函数的图像

可以看到函数 $J(w)$ 是一个凸函数，如果你绘制出 $J(b)$ 图像你将发现它也是凸函数，这也就回答了在1.2节当中的问题，即我们选用 Loss Function 而不是形式更简单的距离函数的原因，距离函数就不是这样的凸函数，它有许多的局部最小值，这不便于我们寻找全局的最优解。

现在假设我们的 $w$ 取在了最低点的右侧，那么你会发现它的斜率是大于零的，也就是公式(11)

\begin{equation} \frac{dJ(w)}{dw}>0 \end{equation}

那么为了减小 $w$ ，你应该用将 $w$ 减去一个常数去乘以这个导数：

\begin{equation} w_{new} = w_{old} - \alpha \frac{dJ(w)}{dw} \end{equation}

这个常数被称作学习率(Learning rate)，一般记作 $\alpha$ ，用来控制每次更新的步幅。而如果我们的 $w$ 偏小了，即取在了最低点的左侧，你会发现它的斜率是小于零的，那么用公式(12)来更新 $w$ 就会使得 $w$ 变大，因此无论 $w$ 偏小还是偏大，我们都可以只使用公式(12)就能够不断地优化 $w$ ，使得 $J(w)$ 越来越小。是不是感觉很神奇?这是使用 $- \alpha \frac{dJ(w)}{dw}$ 作为更新量的一个好处。

另一个好处是，在学习率 $\alpha$ 大小合适的前提下，当初始的 $w$ 差的太远时，因为远处的斜率非常的大，在更新量的促使下 $w$ 会很快被更新到最优点的附近。但这个好处同样也是坏处，当 $w$ 距离最优点很近的时候， $\frac{dJ(w)}{dw}$ 会趋于零， $w$ 的更新会变得非常慢。

对于参数 $w$ ，我们使用公式(12)进行更新，对于参数 $b$ 我不想在这里多写，因为两者是同理的，你不难理解参数 $b$ 的更新公式应该是公式(13)所写的样子，和公式(12)相比就是将所有的 $w$ 换成了 $b$ ，其它保持不变。

\begin{equation} b_{new} = b_{old} - \alpha \frac{dJ(b)}{db} \end{equation}

值得注意的是，对于梯度下降法而言，学习率 $\alpha$ 的选择是至关重要的，一个过小的 $\alpha$ 会使得 $w$ 、 $b$ 更新的过慢，而太大的 $\alpha$ 将导致梯度下降难以收敛。在许多情况下，学习率通常初始设置在 $10^{-2}$ ~ $10^{-4}$ 数量级之间，通过实际的训练情况再进行细微调整，在后面你将看到学习率 $\alpha$ 对整个模型精确度的影响之深。

1.4 Logistic 回归中的梯度下降法

在前面你已经了解了梯度下降法，知道了梯度下降法进行参数优化的原理，即利用损失函数 $J(w,b)$ 是凸函数的特性，通过梯度(斜率)特征调节参数 $w$ 和 $b$ ，并结合学习率 $\alpha$ 控制更新步幅，以引导 $J(w,b)$ 走向全局最低点。下面我们来看看在 Logistic 回归当中的梯度下降法到底是怎样工作的。

梯度下降法更新参数的核心你一定还记得，我们把它摘抄过来并稍作修改：

\begin{equation} w := w - \alpha \frac{\partial J(w, b)}{\partial w} \end{equation}

\begin{equation} b := b - \alpha \frac{\partial J(w, b)}{\partial b} \end{equation}

如果你将上面两个公式与1.3节中给出的更新公式做对比的话，你会发现有两点修改。首先此处使用了 ":=" 符号，如果你之前没有见过这个符号的话也不用担心，它只是表示数据更新，这样就不需要像公式(12)与公式(13)那样总是带着 $_{new}$ 和 $_{old}$ 的角标了。

第二点就是导数符号都修正成了偏导数，因为1.3节当中为了方便讨论所以只考虑了一个量而有意地忽略了另一个量，但实际情况是 $J(w, b)$ 是一个二元函数，对其一个参量求导应该写成偏导的形式。这是对公式(12)和公式(13)的两点修改，希望你能理解。

为了更新参数，我们需要的只是 $\frac{\partial J(w, b)}{\partial w}$ 和 $\frac{\partial J(w, b)}{\partial b}$ ，学习率 $\alpha$ 是我们自己设置的，而 $J(w, b)$ 正是 $L(\hat{y},y)$ 的均值，如果你熟悉链式法则的话，你不难发现实际上我们只需要计算 $\frac{\partial L(\hat{y}, y)}{\partial w}$ 与 $\frac{\partial L(\hat{y}, y)}{\partial b}$ 即可，而本小节的核心正是求解这两个量。

如果你精通微积分，相信你可以很快写出这两偏导数的答案，但是为了便于理解，我们还是在此采用链式法则将求解步骤进行拆分，这也便于引出本小节中的一个重要概念。如果你学过微积分，那么下面的推导过程你应该不难理解，要是你看不懂下面的一堆算式，一头雾水也不用太担心，记住最终的结论也是可以的，这些推导的过程对你在编程实践环节不会造成什么困扰。

为了确保你对链式法则不会太陌生，这里简单地举一个例子：
如果有一串函数， $a = F_1(x), b = F_2(a), c = F_3(b)$ ，此时你想要求 $x$ 关于 $F_3(b)$ 的导数 $\frac{dF_3(b)}{dx}$ ，那么你需要遵循链式法则：

\begin{equation} \frac{dF_3(b)}{dx} = \frac{dF_3(b)}{db} \frac{dF_2(a)}{da} \frac{dF_1(a)}{dx} \end{equation}

如果你不太理解的话，尝试把公式(16)分母中 $b$ 、 $a$ 的值用对应的函数带入：

\begin{equation} \frac{dF_3(b)}{dx} = \frac{dF_3(b)}{dF_2(a)} \frac{dF_2(a)}{dF_1(x)} \frac{dF_1(a)}{dx} \end{equation}

你会发现中间的微分项全部都约掉了，最后得到 $\frac{dF_3(b)}{dx} = \frac{dF_3(b)}{dx}$ 的恒等式，这也说明链式法则是有效的。

首先我们计算一下 $a$ 对于损失函数 $L(a,y)$ 的偏导数 $\frac{\partial L(a,y)}{\partial a}$ ：

\begin{equation} \frac{\partial L(a,y)}{da} = -\frac{\partial}{da}[yloga + (1-y)log(1-a)]\\ = -\frac{y}{a}+\frac{1-y}{1-a} \end{equation}

我们完成了第一步计算，将这个计算在图中标注出来。在下图（图1-8）当中这个计算的结果使用符号 $dL/da$ 来表示，向后的弧形箭头表示从当前单元向后计算输入单元的(偏)导数。

计算图

图1-8 向后计算 $\frac{\partial L(a,y)}{da}$

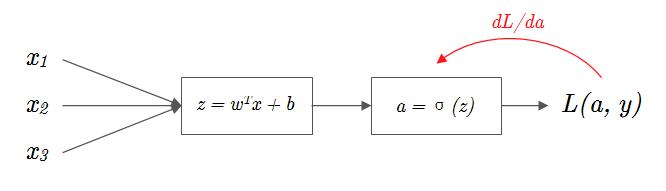
下面类似计算 $\frac{d\sigma(z)}{dz}$ 即 $\frac{da}{dz}$ ，和 $\frac{\partial z(w,b)}{\partial w}$ 、 $\frac{\partial z(w,b)}{\partial b}$

\begin{equation} \frac{d\sigma(z)}{dz} = -\frac{d}{da}(\frac{1}{1+e^{-a}}) = a(1-a) \end{equation}

\begin{equation} \frac{\partial z(w,b)}{\partial w} = -\frac{\partial}{\partial w}(w^Tx+b) = x \end{equation}

\begin{equation} \frac{\partial z(w,b)}{\partial b} = -\frac{\partial}{\partial b}(w^Tx+b) = 1 \end{equation}

最后通过链式法则计算 $\frac{\partial L(\hat{y}, y)}{\partial w}$ 与 $\frac{\partial L(\hat{y}, y)}{\partial b}$ ：

\begin{equation} \frac{\partial L(\hat{y}, y)}{\partial w} = \frac{\partial L(a,y)}{\partial a} \frac{d\sigma(z)}{dz} \frac{\partial z(w,b)}{\partial w} = x(a-y)^T \end{equation}

\begin{equation} \frac{\partial L(\hat{y}, y)}{\partial b} = \frac{\partial L(a,y)}{\partial a} \frac{d\sigma(z)}{dz} \frac{\partial z(w,b)}{\partial b} = (a-y)^T \end{equation}

这样就可以得到我们的目标 $\frac{\partial J(w, b)}{\partial w}$ 和 $\frac{\partial J(w, b)}{\partial b}$ 了，它们就是公式(22)和公式(23)在数据集上的均值，一般使用 $m$ 表示训练集的大小，就有下式：

\begin{equation} dw = \frac{\partial J(w, b)}{\partial w} = \frac{1}{m} \sum_{i=1}^{m}\frac{\partial L(\hat{y}^{(i)}, y^{(i)})}{\partial w} = \frac{1}{m} \sum_{i=1}^{m}[x^{(i)}(a^{(i)}-y^{(i)})^T] \end{equation}

\begin{equation} db = \frac{\partial J(w, b)}{\partial b} = \frac{1}{m} \sum_{i=1}^{m}\frac{\partial L(\hat{y}^{(i)}, y^{(i)})}{\partial b} = \frac{1}{m} \sum_{i=1}^{m}(a^{(i)}-y^{(i)})^T \end{equation}

在写代码的时候，为了简化变量名，通常使用 $dw$ 与 $db$ 来代表 $\frac{\partial J(w, b)}{\partial w}$ 和 $\frac{\partial J(w, b)}{\partial b}$ 。

如果你学过高等数学的话，我十分建议你动笔自己来算一算，这个计算的过程很有趣，看似复杂的表达式，最终却能够得到如此简洁的结果，实则美妙。

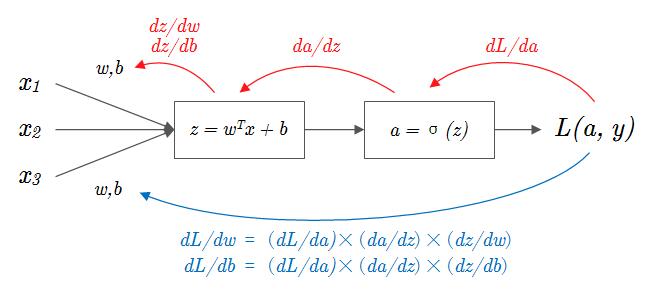
到目前为止，我们已将完成了每一个“链条”的求解，如果在图像上标示出来，这个过程就是图1-9 的上半部分，而图1-9 的下半部分就是通过链式法则将各“链条”相乘得到最终的计算结果，整个图1-9 的过程被称作向后传播(Back-propagation)，又叫反向传播。

Logistic 回归的向后传播过程

图1-9 Logistic 回归的向后传播过程

梯度下降的核心在于参量的更新，也就是更新量的求解。现在，我们已经计算得到了答案（公式(24)和公式(25)），Logistic 回归中的梯度下降法最终被归纳为下面两行：

\begin{equation} w := w - \alpha dw \end{equation}

\begin{equation} b := b - \alpha db \end{equation}

重申一次，如果你对上面的推导过程感到很头疼的话，不用过于担心，记住最后的结论也是没有问题的。

1.5 本篇小结

很棒，你的单层神经网络已经完成了一轮训练！即一次完整的向前传播（图1-5）、向后传播（图1-9）与参数更新（公式(26)(27)）。在实际的神经网络训练过程当中就是通过重复这个过程来不断地迭代参数 $w$ 和 $b$ 使得全局损失函数 $J(w, b)$ 尽可能小，达到“学习”优化的目的。

至此，你已经完成了 Logistic 回归的理论部分学习，在下一篇中你将了解到向量化的相关内容，你将发现在神经网络当中向量化的重要性，以及如何向量化 Logistic 回归、如何向量化 Logistic 回归的梯度输出。

在进入下一篇之前，你可以试着先思考以下几个问题，这些是本篇当中的核心内容：

二元分类问题中的 Logistic 回归是怎样的流程？（图1-9）

为什么要引入 Sigmoid 激活函数？（将 $z=w^Tx+b$ 映射为区间 $[0,1]$ 上的一个概率）

Logistic 回归中使用什么作为损失函数？（Loss Function / Cost Function）

梯度下降法的“下降”核心可以分为哪两部份？（学习率 $\alpha$ 与梯度(斜率)）

Logistic 回归中参数 $w$ 与 $b$ 的迭代公式是？（公式(14)(15) 或公式(26)(27)）

总结

Logistic 回归：Logistic 回归是一种广义上的线性回归，常用于处理二元分类问题。

Sigmoid 函数：Sigmoid 函数将 $z=w^Tx+b$ 映射到区间 $[0,1]$ 上，便于将其视为概率来进行分类。

损失函数：Loss Function 代表单样本损失，Cost Function 代表整体损失均值，用于衡量预测精确度。

梯度下降法：利用损失函数是凸函数的特性，通过梯度(斜率)特征来更新参数 $w$ 和 $b$ ，并结合学习率 $\alpha$ 控制更新步幅，以引导损失函数 $J(w,b)$ 走向全局最低点。

Logistic 回归中对于单样本的参数更新公式：

w := w - \alpha x(a-y)^T

b := b - \alpha (a-y)^T

对于单样本在向前传播中计算了：预测值 $a = \sigma(z)$ 与损失函数 $L(a,y)$ 。

对于单样本在反向传播中计算了：参数 $w$ 和 $b$ 的更新梯度 $x(a-y)^T$ 与 $(a-y)^T$ 。