概述

本篇属于理论篇，你将了解什么是向量化、向量化对神经网络训练优化的重要性，以及如何向量化 Logistic 回归及其梯度输出。

Title

2.0 向量化概述

在前面，你已经认识了 Logistic 回归，并且对梯度下降以及梯度下降是如何工作的有了一个具体的认知。如果你有认真阅读第一篇的话，相信你还记得在第一篇中曾经提到过一个矩阵 $X$，它表示将所有的输入样本在水平方向上堆叠起来，也就是下面这个样子：

$$ \begin{equation} X = \begin{bmatrix} {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ x^{(1)}&x^{(2)}&{\cdots}&x^{(m)}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ \end{bmatrix} _{n_x \times m} \end{equation} $$

为了在后面方便说明，这里将每一个输入样本的下标也标示出来，这样你将看到公式(1)更加完整的形式：

$$ \begin{equation} X = \begin{bmatrix} x^{(1)}_1&x^{(2)}&{\cdots}&x^{(m)}_1\\ x^{(1)}_2&x^{(2)}&{\cdots}&x^{(m)}_2\\ {\vdots}&{\vdots}&{\cdots}&{\vdots}\\ x^{(1)}_{n_x}&x^{(2)}_{n_x}&{\cdots}&x^{(m)}_{n_x}\\ \end{bmatrix} _{n_x \times m} \end{equation} $$

为了确保你明白公式(2)中每一个角标的含义，在这里特别说明一下，使用小括号括起来的上标表示的是样本的编号，而没有用括号括起来的下标代表的是样本的某一个输入，例如对于符号 $x^{(2)}_{n_x}$，它所代表的是训练集中第2个训练样本的第 $n_x$ 个输入，因为 $n_x$ 是指输入的总个数，所以 $x^{(2)}_{n_x}$ 表示的就是第2个训练样本的最后一个输入。

将原本独立的一个个样本组合在一起，构成一个新的矩阵，其实这就是向量化。你可能要问，在上篇中已经实现了 Logistic 回归，使用 $x$ 表示单个样本，在对所有样本逐个计算就足够了，为什么还要使用向量化引入一个样本矩阵 $X$？

2.1 非向量化与向量化实例

试想，如果给你一个给你 1000000 个数据 $a_1$~$a_{1000000}$，以及 1000000 个数据 $b_1$~$b_{1000000}$，要你求每一对 $a_i$ 和 $b_i$ 相乘的结果的总和$c$，你会怎么做？

在接触向量化之前，你应该会想到使用 for 循环，将 $a_i$ 与 $b_i$ 的乘积依次相加，就可以得到结果 $c$ 了，我们来试一下。

使用 for 循环

import numpy as np
import time as t

# 生成 1000000 随机数据
a = np.random.rand(1000000)
b = np.random.rand(1000000)

# for 循环版本
c = 0

# 开始计时
startTime = t.time()

# 循环计算
for i in range(1000000):
    c += a[i]*b[i]
    
# 停止计时
deltaTime = t.time() - startTime

# 输出结果与耗时情况
print("计算结果：" + str(c) + ", for 循环计算耗时：" + str(1000 * deltaTime) + "ms")

以上是使用 for 循环完成要求计算的 python 代码，输出结果是：

计算结果：249879.05298545936, for 循环计算耗时：519.999980927ms

使用向量化

# 向量化版本
c = 0

# 开始计时
startTime = t.time()

#矩阵计算
c = np.dot(a,b)

# 停止计时
deltaTime = t.time() - startTime

# 输出结果与耗时情况
print("计算结果：" + str(c) + ", 矩阵计算耗时：" + str(1000 * deltaTime) + "ms")

以上是使用向量化完成要求计算的 python 代码，输出结果是：

计算结果：249879.05298545936, 矩阵计算耗时：0.999927520752ms

进行多次计算，可以绘制出 for 循环与向量化计算的耗时对比图：

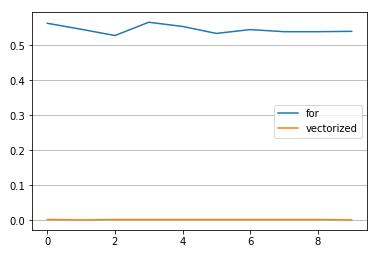
Title

图 1-1 for 循环与向量化计算耗时对比

实在是令人惊喜，正如你所看到的，向量化版本没有使用 for 循环就正确完成了所有计算，并且计算的代码量只有一行，而仅针对简单的乘法与加法运算而言，向量化计算的效率就要比 for 循环高出 500 倍上下，在其他更加复杂的运算下，这个差距还会拉得更大。可以看到，无论从简洁性还是从效率的角度讲，向量化计算几乎是完美的。

因此，不管是在什么算法当中，如果能够不使用 for 循环就尽量不要使用 for 循环，其效率实在是太糟糕了。在神经网络的训练过程中，效率显得尤为重要，面对数量巨大的训练样本，向量化你的模型是非常有必要的，它能够大量地节约你的时间去做更多的训练，或是做参数的调整。

2.2 向量化 Logistic 回归

在前面你已经见识到了向量化威力，通过向量化你能够实现数据的并发计算，进而为你节约大量的时间。下面，我将用伪代码给出 Logistic 回归非向量化版本，即使用 for 循环编码实现上一篇当中的理论模型，你可以直接阅读代码，并思考如何向量化这个过程。

for 循环版本

1 | $for$ $i$ $=$ $1$ $to$ $m$

2 | ${$

3 | $z^{(i)}$ $=$ $w^Tx^{(i)}$ $+$ $b$ # 计算线性输出

4 | $a^{(i)}$ $=$ $\sigma(z^{(i)})$ # 映射到 $[0,1]$

5 | $J$ $+=$ $L(a^{(i)},y^{(i)})$ # 记录 Loss Function 的累加

6 | $dz^{(i)}$ $=$ $a^{(i)}-y^{(i)}$ # 计算 $\frac{\partial L(a,y)}{\partial a} \frac{d\sigma(z)}{dz}$ (前两段"链条"的乘积)

7 | $for$ $j$ $=$ $1$ $to$ $n_x$

8 | $dw_j$ $+=$ $x^{(i)}_jdz$ # 累加 $dw$

9 | $db$ $+=$ $dz$ # 累加 $db$

10 | $}$

11 | $for$ $j$ $=$ $1$ $to$ $n_x$

12 | $dw_j$ $=$ $dw_j/m$ # 计算每个输入的 $dw$

13 | $db$ = $db/m$ # 计算 $db$

14 | $J$ = $J/m$ # 计算 $Cost Function$

可以看到，在这段代码中出现了三个 for 循环，甚至出现了循环嵌套，这对算法效率的影响是很大的。如果你试着读上面的代码并结合注释，能够理解每一行代码在做些什么的话最好了。如果你觉得以你目前的思维将模型投射到代码还是有些困难也没有关系，我们来逐行解读代码，并一步步地将其向量化。

在这里，向量化的过程其实就是消除 for 循环的过程，我们从最里层的 for 循环开始。你看到了，最里层的 for 循环也就是 7 到 8 行，在 11 到 12 行也有一个小小的 for 循环，我们先从 7 到 8 行的 for 循环开始。

7 | $for$ $j$ $=$ $1$ $to$ $n_x$

8 | $dw_j$ $+=$ $x^{(i)}_jdz$ # 累加 $dw$

如果你还是觉得这个通式太抽象地话，我们可以将这个 for 循环一条条详细地列出来：

$$ dw_1 += x^{(i)}_1dz $$

$$ dw_2 += x^{(i)}_2dz $$

$$ \vdots $$

$$ dw_{n_x} += x^{(i)}_{n_x}dz $$

仔细看一看，你有没有发现向量化的影子？

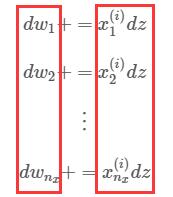
for 循环展开

图 1-1 for 循环展开

这简直就是天然的矩阵形式！我们只需将等式左侧的所有 $dw_{...}$ 封装进一个列矩阵 $dw$ 即可，等式的右侧也是同理，所有的 $x^{(i)}_{...}$ 可以封装进一个列矩阵 $x^{(i)}$，即：

$$ \begin{equation} dw = \begin{bmatrix} dw_1\\ dw_2\\ {\vdots}\\ dw_{n_x}\\ \end{bmatrix} _{n_x \times 1} , x^{(i)} = \begin{bmatrix} x^{(i)}_1\\ x^{(i)}_2\\ {\vdots}\\ x^{(i)}_{n_x}\\ \end{bmatrix} _{n_x \times 1} \end{equation} $$

这时你会惊喜地发现，整个循环操作直接被简化成为了一行极其简短的矩阵运算！

$$ \begin{equation} dw += x^{(i)}dz \end{equation} $$

至此，我们已经迈出了向量化的第一步，成功消除了代码中的一个 for 循环。下面我们继续看一看第二个即代码中 11 到 12 行的 for 循环。使用同样的方法，如果将其展开的话，你会发现这个 for 循环其实在做如下的重复性劳动：

$$ dw_1 = dw_1/m $$

$$ dw_2 = dw_2/m $$

$$ \vdots $$

$$ dw_{n_x} = dw_{n_x}/m $$

我相信这一次你已经可以一眼看出如何将其向量化了，你会发现这个过程其实真的很简单，只需要将等式左侧的循环变量封装进一个列矩阵 $dw = [dw_1,dw_2,\cdots,dw_{n_x}]^T$，这个循环就被简化成为了下面一行代码：

$$ \begin{equation} dw = dw/m \end{equation} $$

不知道你发现没有，到现在为止，我们已经完成了所有输入的向量化，我们没有使用一个 for 循环就处理了所有输入系数 $w$ 的 $dw$ 计算，如果你觉得自己对 for 循环向量化的过程已经有所领会的话，建议你到此停下来，自己尝试将第一层也是最大的一层 for 循环也完成向量化，如果你能做到的话，你就实现了不使用一个 for 循环并一口气完成所有样本的训练。

下面我们来看最外一层的样本循环，首先第一条是线性组合的计算：

3 | $z^{(i)}$ $=$ $w^Tx^{(i)}$ $+$ $b$

先等一下，你可能会像之前一样将循环展开来看一看，之后得到封装的矩阵，最后用矩阵去替换原来的整列。但是其实你会发现你需要做的仅仅是将所有的循环变量替换掉，而不需要每一次都展开来看了。就比如上面这个第 3 行代码，它的循环变量是 $z^{(i)}$ 与 $x^{(i)}$，识别的方法就是它们带有这一层循环的变量 $i$，将其直接替换为 $Z$ 与 $X$，你就得到了最终结果：

$$ \begin{equation} Z = w^TX + b \end{equation} $$

你只需要在心里记得与明白， $Z$ 和 $X$ 是循环产生的列就好(公式(7))，也就是图1-1 那样的形式，那是它的由来，但在实际向量化的过程中，你并不需每次都像那样展开一下再去替换，只要你对这个过程明了，那么直接写出结果就行了。

$$ X = \begin{bmatrix} {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ x^{(1)}&x^{(2)}&{\cdots}&x^{(m)}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ \end{bmatrix} _{n_x \times m} , \begin{equation} Z = \begin{bmatrix} z^{(1)}&z^{(2)}&{\cdots}&z^{(m)}\\ \end{bmatrix} _{1 \times m} \end{equation} $$

同理，第 4、5、6 行的向量形式应该分别是公式(8)(9)(10)所示：

$$ \begin{equation} A = \sigma(Z) \end{equation} $$

$$ \begin{equation} J = -(1/m)(YlogA + (1-Y)log(1-A)) \end{equation} $$

$$ \begin{equation} dZ = A - Y \end{equation} $$

其中：

$$ \begin{equation} A = \begin{bmatrix} a^{(1)}&a^{(2)}&{\cdots}&a^{(m)}\\ \end{bmatrix} _{1 \times m} \end{equation} $$ $$ \begin{equation} Y = \begin{bmatrix} y^{(1)}&y^{(2)}&{\cdots}&y^{(m)}\\ \end{bmatrix} _{1 \times m} \end{equation} $$

至此，整个 for 循环版本都被我们向量化了，下面你看到的就是 Logistic 回归及其梯度输出的向量化版本：

向量化版本

1 | $Z$ = $w^TX$ $+$ $b$

2 | $A$ = $\sigma(Z)$

3 | $J$ = $-(1/m)(YlogA$ $+$ $(1-Y)log(1-A))$

4 | $dZ$ = $A$ $-$ $Y$

5 | $dw$ = $(1/m)XdZ^T$

6 | $db$ = $(1/m)dZ^T$

甚至，由于你在写代码的过程中并不需要将中间量写出来，因此你可以得到下面这个更简的版本：

1 | $A$ = $\sigma(w^TX$ $+$ $b)$

2 | $J$ = $-(1/m)(YlogA$ $+$ $(1-Y)log(1-A))$

3 | $dw$ = $(1/m)X(A$ $-$ $Y)^T$

4 | $db$ = $(1/m)(A$ $-$ $Y)^T$

你没看错，只有短短的四行！并且这四行精简的代码是一次性并行完成整个数据集上所有样本的训练！现在你可以想象，假如没有经过向量化操作，直接用嵌套的 for 循环去训练基数庞大的海量数据，不仅代码繁杂，效率上更将是多么可怕的一件事。向量化技术极大的提升了神经网络的训练的效率，也正因如此，向量化才在神经网络与深度学习当中具有重要的意义。

2.3 本篇小结

经过向量化后的 Logistic 回归，并没有使用一个 for 循环，我们只用四行极简的代码，抽象了上一篇中上万字的复杂过程，我想你也不得不为向量化与矩阵运算的强大而感慨了。

至此，你已经完成了向量化的理论部分学习，在下一篇里，你将在实战中看到向量化 Logistic 回归及其梯度输出的落地实现，即猫图的识别。你将看到单层神经网络的模块化开发与如何一步步编写代码，动手搭建一个自己的神经网络，并使它完整的工作起来。

在进入下一篇之前，你可以试着先思考以下几个问题，这些是本篇当中的核心内容：

在第一篇中已经建立了 Logistic 回归模型，还有必要做向量化工作吗？（有必要）

向量化后的 Logistic 回归能够一次性完成所有样本的一次训练，并完成参数的一次迭代，正确或错误？（正确）

下面是向量化版本的 Logistic 回归与梯度输出，其中哪几行实现的是向前传播？哪几行实现的是向后传播？（向前1、2行；向后3、4行） 1 | $A$ = $\sigma(w^TX$ $+$ $b)$ 2 | $J$ = $-(1/m)(YlogA$ $+$ $(1-Y)log(1-A))$ 3 | $dw$ = $(1/m)X(A$ $-$ $Y)^T$ 4 | $db$ = $(1/m)(A$ $-$ $Y)^T$

试用向量化技术将下面代码简化成一行，其中 $Fun(a,b) = a + b$，$k_i$ 与 $\mu_i$ 是维度相同的矩阵（$var=(1/n)(k+\mu)$） 1 |$for$ $i$ $=$ $1$ $to$ $n$ 2 | $var_i$ $+=$ $Fun(k_i,\mu_i)$ 3 |$for$ $i$ $=$ $1$ $to$ $n$ 4 | $var_i$ $=$ $var_i/n$

使用鼠标选中括号内容以查看答案。

总结

向量化的意义：实现循环操作的并行化。

向量化后的 Logistic 回归模型及其梯度输出：

$A = \sigma(w^TX + b)$ $J = -\frac{1}{m}(YlogA + (1-Y)log(1-A))$ $dw = \frac{1}{m}X(A - Y)^T$ $db = \frac{1}{m}(A - Y)^T$