
多视角探析贝塞尔曲线匀速化技术、实现及其应用
概述
就在三年前,我于CSDN博客上发布了一篇题为《贝塞尔曲线运动n阶追踪方程的数学原理及其匀速化方法和应用》的博客文章,主要探讨的是贝塞尔曲线由一阶至n阶在数学层面的生成过程,以及匀速化的一些问题。不过当时博文中的“匀速化”似乎存在歧义,有朋友反馈匀速化后仍不匀速,后经了解才发现此匀速化非彼匀速化。本文尝试区分探讨两种匀速化及各自的应用场景和实现方法。

一、匀速化与“匀速化”
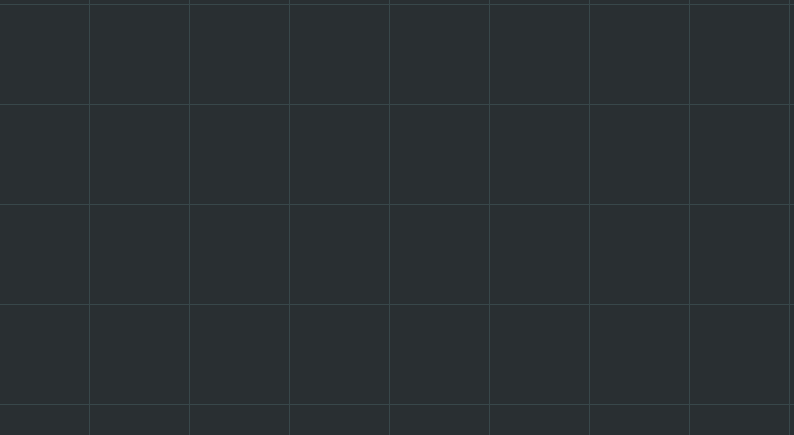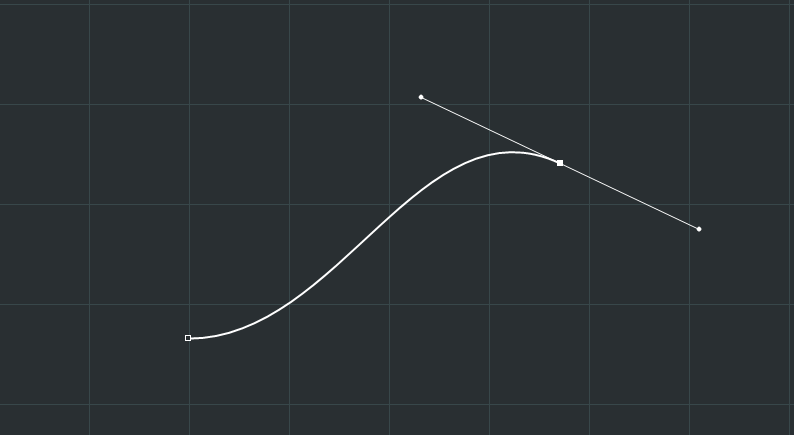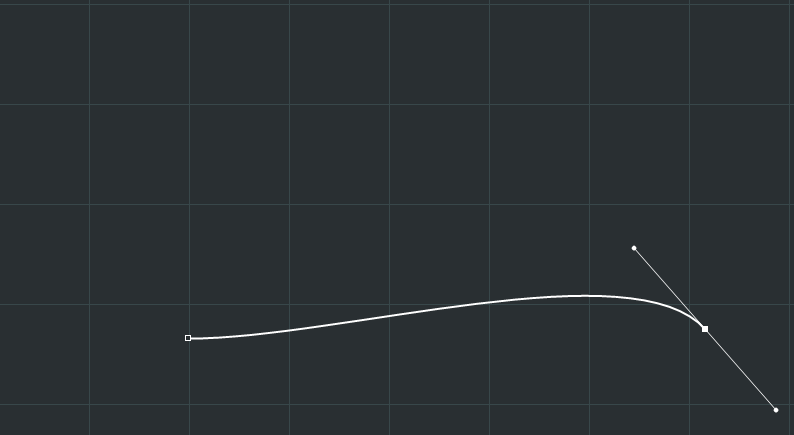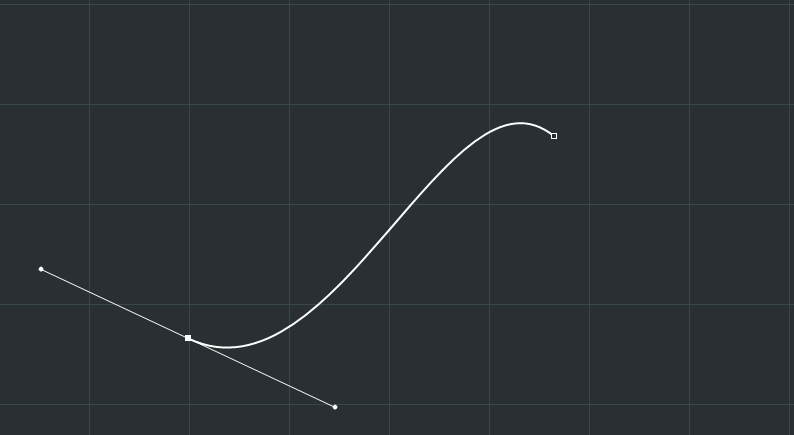
这,就是贝塞尔曲线,三阶的。在之前的博文中,你已经见过了n阶形态的数学推导,应该来说,贝塞尔曲线的生成模式还是相当的简洁和符合直觉的,除了其三阶常常应用为各矢量绘图软件中的钢笔工具之外,还有相当多的地方需要用到它。
1. 路径(生成)匀速化
一个方面就是路径匀速化,或者说生成匀速化。例如在GTA5、2077等各种类型的可行走的游戏当中,并不是所有的道路都是横平竖直的,道路可能是弯曲的,尤其是在赛车游戏中,各种曲线赛道和弯道几乎无处不在,又如潜行类游戏中,NPC 沿着固定曲线路径匀速行走。那么这就带来了一个问题,如何让 NPC 在曲线道路上匀速地行走?,也即如何匀速地生成一条贝塞尔曲线。在这个角度下,一条贝塞尔曲线的横轴与纵轴均表示实体位置,如横轴代表水平坐标 x,纵轴代表垂直坐标 y,曲线上的任意点的含义是目标实体的真实相对位置。

2. 缓动匀速化
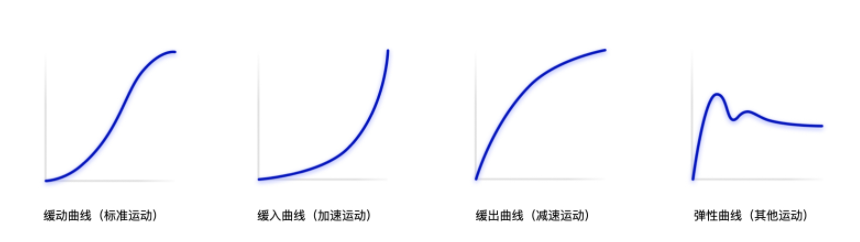
另一方面则是缓动匀速化,在这个角度下,贝塞尔曲线的横轴不是实体的横坐标,而是时间,纵轴也不是实体的纵坐标,而是位移。缓动匀速化旨在实现让实体获得符合贝塞尔曲线规律的运动效果。
好,下面我们就来分别探讨一下这两种匀速化的细节,如何实现这两种匀速化,以及两种匀速化都由什么意义和应用吧。
二、路径匀速化
1. 技术难点
之前说到,路径匀速化说白了就是如何实现让 NPC 在曲线道路上匀速地行走。
这个问题看上去很蠢,因为直接让 NPC 匀速运动不就好了。对于一条水平的或者垂直的或者斜率恒定的直线来说,确实很好实现。例如对于一条斜率为 45° 的直线路径,只需要想好 NPC 行走的速度 v,然后每隔一个固定的时间差 t 让 NPC 分别在水平和垂直方向上的位移增加 vtcos\theta 和 vtsin\theta 即可。
但是曲线运动或许没有这么简单,首先,曲线上的 \theta 并不是固定的度数,因此要写出一个固定的形如 \Delta x = vsin\theta \Delta t 并不容易,其次贝塞尔方程是时间 t 到坐标 (x, y) 的映射,而实际上计算机代码本身就不是匀速执行的,因此想要获得匀速的 t 本身就不是一件容易的事情。
要理解这一点,我们可以先从直线开始。如果你对贝塞尔公式熟悉的话,不难知道直线其实可以看作是一阶的贝塞尔曲线。因此我们先从一阶入手,看看匀速化贝塞尔是不是真的那么轻松和符合直觉。
我们先来看一看按照 “这个问题看上去很蠢” 的一般性思路来解决这个问题,即简单粗暴设置一个 Timer,经每个固定的时间间隔累计当前已流逝的时间 sum\_t,再设置一个期望的完成运动的总时间 total\_t,将两者作商即得到当前时刻处于整个运动时间中的比例位置:
按照常理来讲,我们只需要将运动的始末点坐标和这个 timeRate 带入贝塞尔公式中即可得到此时刻对应的点的坐标。而我们设置的定时器的 Interval 是固定的,那么得到的点的运动也就应该是恒定的。
private void timerHandlerThread()
{
// 设置计划花费 timeFull 的时间走完目的路径
if (timeSigma <= timeFull)
{
// 设置一个点坐标,作为我们 t 时刻运动到的位置
Point unrealPoint = new Point();
// 累计时钟周期,得到当前经过的总时间
timeSigma += timer1.Interval;
// 贝塞尔时间域在 [0,1],将当前经过的时间除以计划时间带入得当前位置坐标
unrealPoint = b3.b3_c(p, timeSigma / timeFull);
// 绘制当前位置及在 x、y 轴上的投影
lock (this)
{
// x
g.DrawRectangle(pen, new Rectangle(unrealPoint.X - 1, p[0].Y - 1, 2, 2));
// y
g.DrawRectangle(pen, new Rectangle(p[0].X - 1, unrealPoint.Y - 1, 2, 2));
// CurveMotion
g.DrawRectangle(pen, new Rectangle(unrealPoint.X - 2, unrealPoint.Y - 2, 4, 4));
}
}
}
下面我们看一看这种非常符合直觉的方案的运行结果。

很可惜,理想和现实还是有差距的,不难看出这种看似十分符合直觉的匀速化方法得到的曲线生成过程,或者说曲线运动,根本不是匀速的,而是两头慢,中间快(两头的生成点更加密集,速度更慢,中间生成点更加稀疏,速度更快)。
思考片刻,你或许会质疑:也许是 timerHandlerThread 的调用本身是不匀速的?你在不匀速调用的函数里累增恒定的 timer1.Interval,结果肯定不匀速啊!好,那我们就不增静态的周期值,而是每次调用时实时计算已流逝的时间取而代之再看看:
private void timerHandlerThread()
{
// ts 在开始生成时初始化为 DateTime.Now - DateTime(1970, 1, 1, 0, 0, 0, 0)
TimeSpan ts2 = (DateTime.Now - new DateTime(1970, 1, 1, 0, 0, 0, 0)) - ts;
// 从开始运动到执行这条代码时经过的总时间
timeSigma = ts2.TotalMilliseconds;
// 设置计划花费 timeFull 的时间走完目的路径
if (timeSigma <= timeFull)
{
// 设置一个点坐标,作为我们 t 时刻运动到的位置
Point unrealPoint = new Point();
// 贝塞尔时间域在 [0,1],将当前经过的时间除以计划时间带入得当前位置坐标
unrealPoint = b3.b3_c(p, timeSigma / timeFull);
// 绘制当前位置及在 x、y 轴上的投影
lock (this)
{
// x
g.DrawRectangle(pen, new Rectangle(unrealPoint.X - 1, p[0].Y - 1, 2, 2));
// y
g.DrawRectangle(pen, new Rectangle(p[0].X - 1, unrealPoint.Y - 1, 2, 2));
// CurveMotion
g.DrawRectangle(pen, new Rectangle(unrealPoint.X - 2, unrealPoint.Y - 2, 4, 4));
}
}
}

可以看到,将策略改为实时计算当前时刻并不奏效,实际上和直接累增时钟周期的做法几乎没有差别。造成这种现象的根本原因在于输入时间的匀速与曲线上点的匀速压根不是一回事儿。
事实上,为了实现点的匀速行进,我们的关注点应该放在合速度关于时间的积分上。也即我之前在《贝塞尔曲线运动n阶追踪方程的数学原理及其匀速化方法和应用》一文中所提及的化曲为直的思想。只要我们求出贝塞尔曲线的总长度,就可以将其拉为一根直线,而后设置一个恒定的速度 v,这样就可以利用之前提到的 \Delta x = v \Delta t 来靠谱地计算真正匀速情况下实体所处的位置了!
不过这个位置是将贝塞尔拉直放平后的那条线上的位置,我们将其记为 X,这样一来,我们只需求得一个参数 t 使得贝塞尔曲线在 [0,t] 上的弧长恰好等于或者相当接近于物体在拉直放平后贝塞尔上的直线位移 X 即可,这个参数 t 就是在特定时刻下匀速贝塞尔对应的真实的匀速的 t,我们记之为 rt(即 real time),也即找到一个 rt 使得对于一个特定的 t 满足:
此时再回头看,你便会恍然大悟为什么之前匀速的时间得不到匀速的运动了,根本原因就在于之前的时钟周期法和实时计算法,都是误以为有下式成立:
即 rt = t,而实际上并不存在这一层关系。好,理清楚了之前的误区,那么问题来了,vt 好算,但如何求 \int_{0}^{rt} B_3(t) dt?下式是三阶贝塞尔曲线方程,t 为时间参数,P 是控制点的坐标,如何求贝塞尔曲线的弧长?
2. 基于辛普森积分法的路径匀速化
辛普森积分法是一种用抛物线近似函数曲线来求定积分数值解的方法。把积分区间等分成若干段,对被积函数在每一段上使用辛普森公式,根据其在每一段的两端和中点处的取值近似为抛物线,逐段积分后加起来,即得到原定积分的数值解。辛普森积分法比梯形法则更精确,二者都是牛顿-柯特斯公式(Newton-Cotes)的特例。——百度百科
要算贝塞尔曲线的弧长,我们可以尝试辛普森积分法。利用辛普森积分法,要求定积分 \int_{a}^{b} f(x) dx (a<b),
则将闭区间等分成 2n 个小区间
在每个小区间上,将抛物线近似成函数f(x)的曲线。设y_i = f(x_i),则可以得到近似值:
我们将生成曲线视作是运动的迹,那么求贝塞尔曲线的弧长自然要对贝塞尔曲线迹的速度求积分,也就是此处辛普森积分中的 f(x) 为贝塞尔曲线的合速度方程。
不难推导三阶贝塞尔的方向速度函数为
进而合速度 v = \sqrt{v_x^2 + v_y^2},有了速度方程,即可使用辛普森积分法求速度函数的积分,得 t 时刻的近似弧长了!方向速度函数及合速度函数的编码较简单,这里给出辛普森积分部分的代码:
// 求 0~t 段的三阶贝塞尔曲线长度
public double beze_length(Point[] p, double t)
{
int TOTAL_SIMPSON_STEP = 1000; // 总分段步数
int stepCounts;
int halfCounts;
int i = 0;
double sum1 = 0, sum2 = 0, dStep = 0;
// 总步数乘以当前时间(0~1)得到参数 t 对应的步数
stepCounts = (int)(TOTAL_SIMPSON_STEP * t);
if (stepCounts == 0)
return 0;
// 化为奇数
if (stepCounts % 2 == 0)
stepCounts++;
// 总步数的一半
halfCounts = stepCounts / 2;
// 每次递增的步数
dStep = t / stepCounts;
// 下面全部代码就是套辛普森积分公式的过程
while (i < halfCounts)
{
// t = (2 * i + 1) * dStep 时贝塞尔曲线的速度
sum1 += beze_speed(p, (2 * i + 1) * dStep);
i++;
}
i = 1;
while (i < halfCounts)
{
// t = 2 * i * dStep 时贝塞尔曲线的速度
sum2 += beze_speed(p, 2 * i * dStep);
i++;
}
return ((beze_speed(p, 0) + beze_speed(p, 1) + 4 * sum1 + 2 * sum2) * dStep / 3);
}
好!现在我们成功实现了贝塞尔曲线弧长函数,回头看看,我们的目标是解出
下面的工作就很轻松了,对于一个目标弧长,我们想要求出一个 rt 对应这个弧长,只需将 rt 初始化为任意数,而后粗暴地二分即可!
public double t2rt_by_baze_length(Point[] p, double length)
{
// 将 rt 初始化为 0
double realTime = 0;
// rt 对应的弧长初始化为 0
double rt_length = 0;
// 与真实弧长的差距
double deltaLength = 0;
// rt 的更新量
double deltaTime = 0;
// 界定二分上下限
double low = 0, high = 1;
do
{
// 半分
if (deltaLength > 0)
{
// rt 对应的弧长太大了,减小 rt
realTime -= (double)(realTime - low) / 2;
// rt 更新幅度
deltaTime = realTime - low;
}
else
{
// rt 对应的弧长太小了,增大 rt
realTime += (double)(high - realTime) / 2;
// rt 更新幅度
deltaTime = high - realTime;
}
// 计算弧长差值
rt_length = beze_length(p, realTime);
deltaLength = rt_length - length;
// 更新二分上下限
if (deltaLength > 0) high = realTime;
else low = realTime;
// 0.01 的误差已经很小了,可视为此时的 rt 就是真实的 rt
// 或者 rt 的更新量足够小时也应跳出,防止梯度消失造成死循环
} while (Math.Abs(deltaLength) > 0.01 && deltaTime >0.00000000000000001);
// 算法收敛
return realTime;
}
终于,我们可以将贝塞尔匀速运动直接视为极简的直线段上的匀速运动了,直接定义一个恒定的速率(由时钟周期体现),然后恒定地累增恒定的位移吧!将匀速变化的当前弧长传给 t2rt_by_baze_length,就能得到对应匀速化贝塞尔曲线的真实的参数 rt 了!
private void timerHandlerThread()
{
if (timeSigma <= timeFull)
{
Point realPoint = new Point();
// ts 在开始生成时初始化为 DateTime.Now - DateTime(1970, 1, 1, 0, 0, 0, 0)
TimeSpan ts2 = (DateTime.Now - new DateTime(1970, 1, 1, 0, 0, 0, 0)) - ts;
// 从开始运动到执行这条代码时经过的总时间
timeSigma = ts2.TotalMilliseconds;
lock (this)
{
// length由运动开始时直接调用三阶贝塞尔弧长计算函数,传入t=1得到,即总弧长
double rt = b3.t2rt_by_baze_length(p, length * timeSigma / timeFull);
realPoint = b3.b3_c(p, rt);
// x
g.DrawRectangle(pen, new Rectangle(realPoint.X - 1, p[0].Y - 1, 2, 2));
// y
g.DrawRectangle(pen, new Rectangle(p[0].X - 1, realPoint.Y - 1, 2, 2));
// CurveMotion
g.DrawRectangle(pen, new Rectangle(realPoint.X - 2, realPoint.Y - 2, 4, 4));
}
}
}
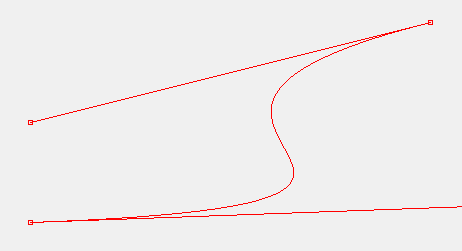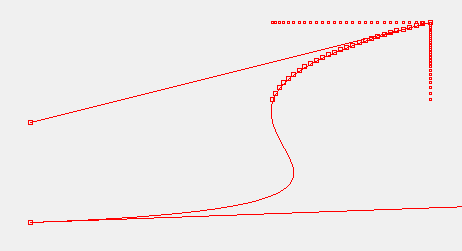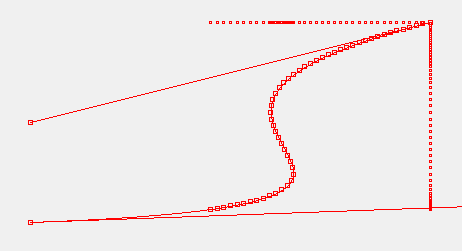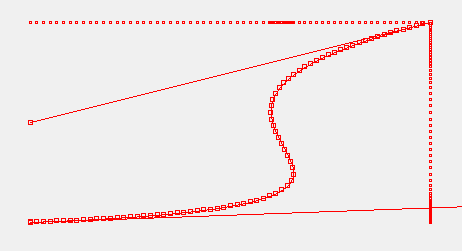
运行效果见下图。至此,我们已经成功实现了曲线的匀速生成,即路径贝塞尔匀速化。

现在改变贝塞尔控制点的坐标,可得本文算法在三阶曲线下的效果:

可以看到,每个生成点在曲线上的间距(弧长)是一致的,且弧长误差控制在0.01内,精度已经相当高。接下来只需要加快速度(可由时钟周期与计划总时长共同控制),即可实现如 NPC 在曲线路径上匀速运动,且只需通过贝塞尔控制点来随意调节运动曲线,无需修改算法代码,如需得到逆向运动,只需反转贝塞尔点,即第 i 个点作为第 n-i-1 个点(i=0,1,2,··· 且 i<n)。
3. 应用实例
具体应用我就不单独写了,以前面提到的 NPC 循环走路为例,即 NPC 巡逻,只需调整好 NPC 行动的贝塞尔曲线,而后 NPC 在到达目标点(t=1)时让其等待一会儿后逆转贝塞尔点,将 t 重置为零即可实现简单的 NPC 巡逻,演示如下:


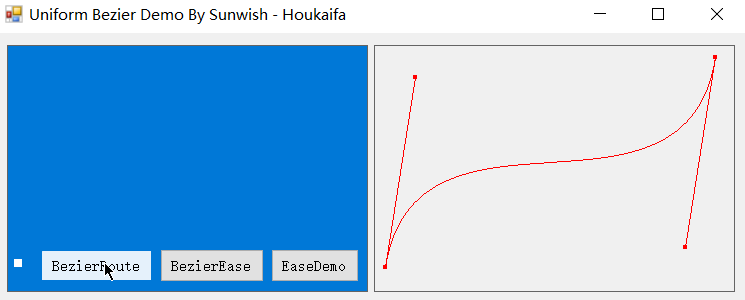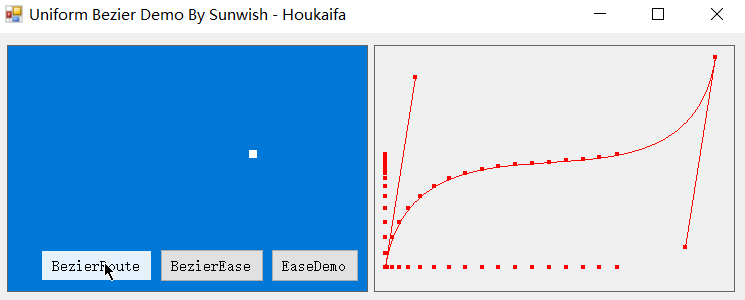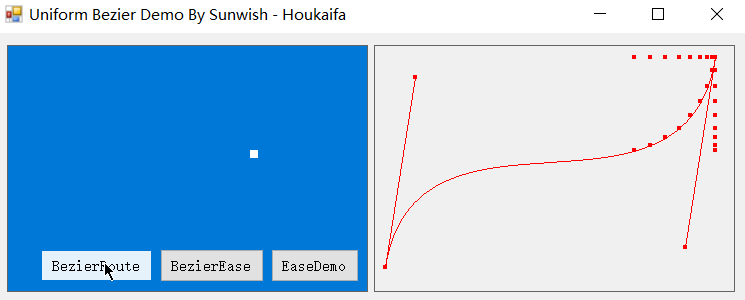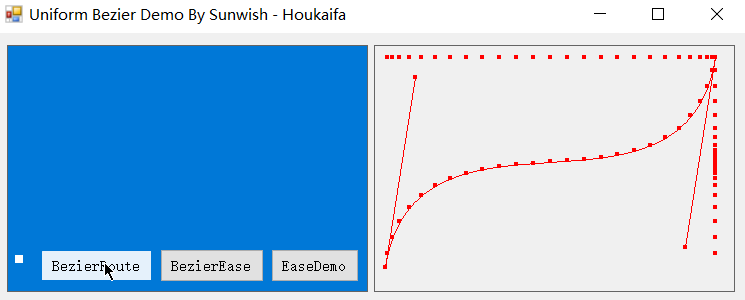
当然说到游戏,我猜想这些底层工作大多游戏引擎应该是会帮开发者封装好的,不过在游戏之外的其它场景若需要用到曲线路径匀速扫描的话,还是自己吃透原理才能得心应手。
好的,接下来让我们从另一个角度看看贝塞尔“匀速化”,或者说另一个层面的“匀速化”——贝塞尔缓动匀速化。
三、缓动匀速化
1. 非匀速化的贝塞尔缓动
在缓动匀速化中,非匀速的情况与路径匀速化中的非匀速情况是完全一致的,不过此处我们的匀速化目标不再是路径生成的匀速化了,而是水平方向上的匀速化。让我们回顾一下非匀速化的情况:

在缓动视角下的贝塞尔匀速化中,我们将一条贝塞尔曲线放在笛卡尔坐标系中,横轴记为时间比率(0~1),纵轴记为位移,即我们需要求得匀速化的时间比率变化(即均匀的横轴输入),进而映射出符合曲线的时间-位移映射。
在贝塞尔缓动中,因为我们将横轴视作是时间轴 t 了,因此要得到匀速的贝塞尔也就是要得到匀速变化的横轴,而之所以出现“匀速化”的时间传入得不到均匀的横轴变化,归根结底是因为纯粹的贝塞尔横轴的意义压根就不是时间 t,而是前面我们在路径匀速化中所聊的路径贝塞尔中的“横坐标”。
因此要得到缓动视角下的匀速贝塞尔,你得尝试转换一下思维了。
2. 逼值法(二分法)实现缓动匀速化
为了得到缓动贝塞尔视角下的匀速时间,你需要将平时意义下的匀速时间 t 传入贝塞尔方程,求得一个横坐标 x,但是注意,这个 x 是那一个世界的 "t",并且经过贝塞尔函数的“扭曲”后,这个世界的匀速的 t 在那个世界对应的 x 并不是那个世界匀速的 x。这可能有点儿绕,不过仔细想一想还是很好理解的。
现在需要做的就是拿着手中现实意义的 t 去寻找贝塞尔映射另一头 x 对应的真正的匀速的 t,即这一头的对应那一头匀速 x 的 t,同路径匀速化一样,我们也将其记作 rt(即real time)。
下面我们就通过二分法来实现 t 到 rt 的转换:
public double t2rt(Point[] p, double t)
{
// 定义真实时间与差时变量
double realTime, deltaTime = 0;
// 曲线上的 x 坐标
double bezierX;
// 计算 t 对应曲线上匀速的 x 坐标
double x = p[0].X + (p[3].X - p[0].X) * t;
double low = 0, high = 1;
realTime = 0.5;
int intT = 0;
do
{
// 半分
if (deltaTime > 0)
realTime -= (double)(realTime - low) / 2;
else
realTime += (double)(high - realTime) / 2;
// 计算本此 "rt" 对应的曲线上的 x 坐标
bezierX = b3(p, realTime);
// 计算差时
deltaTime = bezierX - x;
// 界定二分上下限
if (deltaTime > 0) high = realTime;
else low = realTime;
}
// 差时逼近为0时跳出循环
while (Math.Abs(deltaTime) > 0.0000000000001);
return realTime;
}
这样转换得到的 rt 对应的就是匀速变化的 x 了。有趣的是,如果你观察我们求出来的 rt 的话,你会发现在我们这一头 rt 压根就不匀速,可是一旦经贝塞尔映射后,就成为了匀速的 x,即另一个世界的匀速,请看:

怎么样,是不是很有意思?我们成功得到了均匀的 x!不过现在的贝塞尔曲线是一条简单的直线,我们可以尝试改变贝塞尔曲线的控制点来看看真实曲线下的效果了:

可以看到,水平输入仍旧是匀速的!而若我们将注意力放在纵轴上的生成点上,你会发现纵轴上点的生成密度与曲线斜率趋势完全一致,而**横轴是均匀变化的,即纵轴的位移输出完全匹配了匀速时间对应的贝塞尔曲线。**不过注意,这里的匀速是缓动匀速,不是真正意义上的匀速贝塞尔(即生成匀速化)。
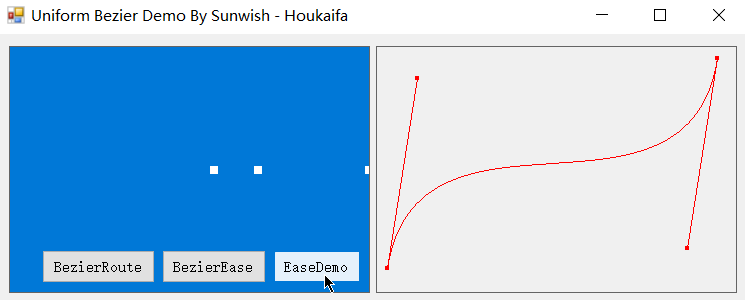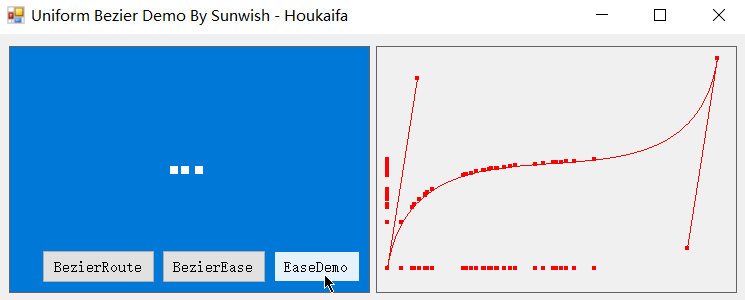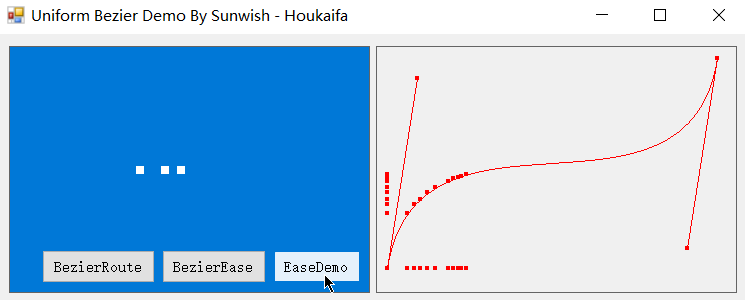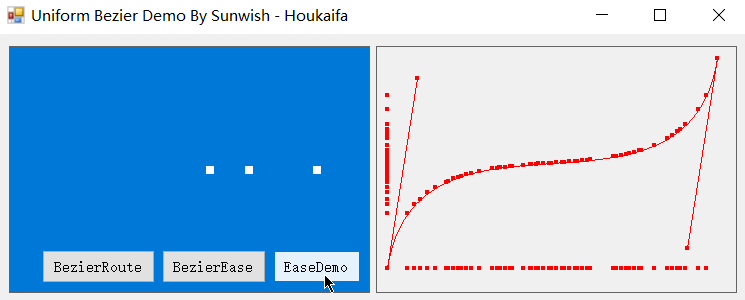
不过在缓动领域中,这种匀速化才正是我们所需要的,利用匀速化后的缓动贝塞尔曲线,我们可以实现动效的轻松调整,下面是基于本篇缓动贝塞尔匀速化算法实现的缓动动效。
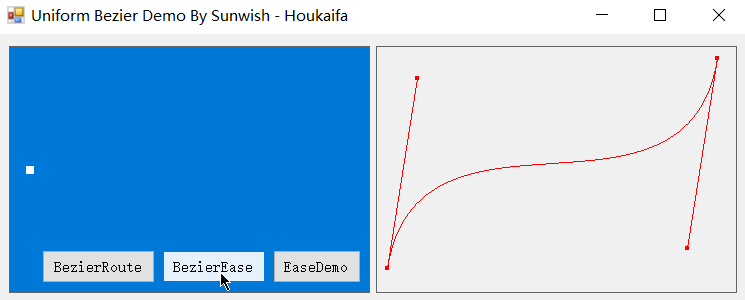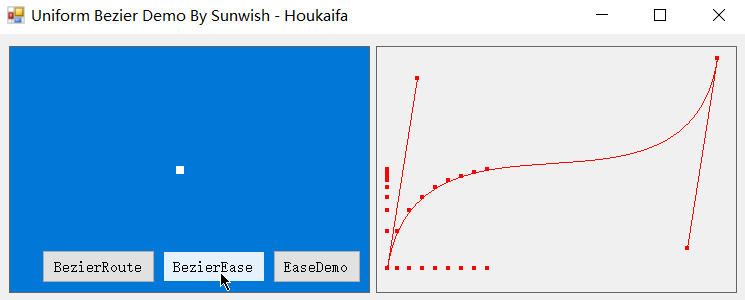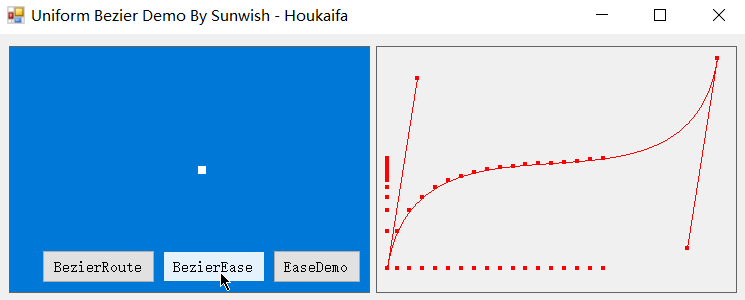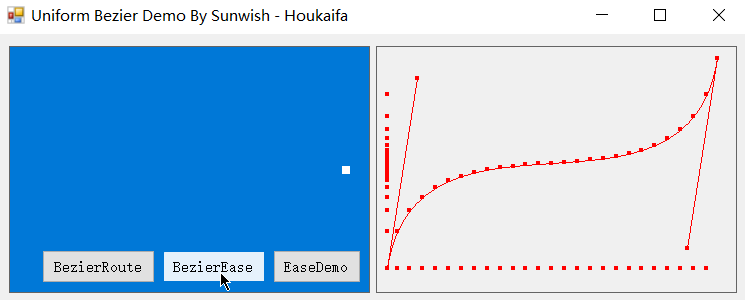
3. 应用实例
没错,下面几个丝滑无比的实例就都是基于匀速化后的缓动贝塞尔曲线的缓动动效,也是基于我正在开发的 Easecurve 缓动引擎项目构建的动效实例。


四、小结
当然,将路径匀速化与缓动匀速化相结合也是极好的,即沿着贝塞尔路径做指定贝塞尔缓动,结合演示如图:
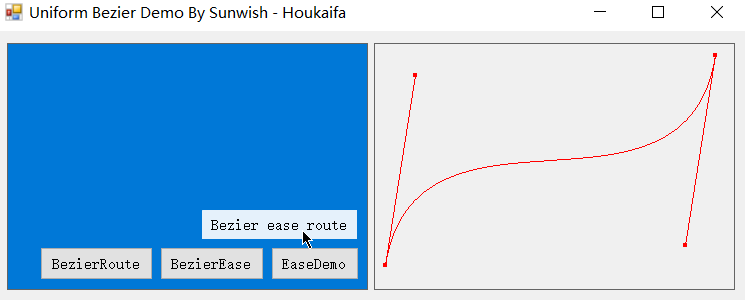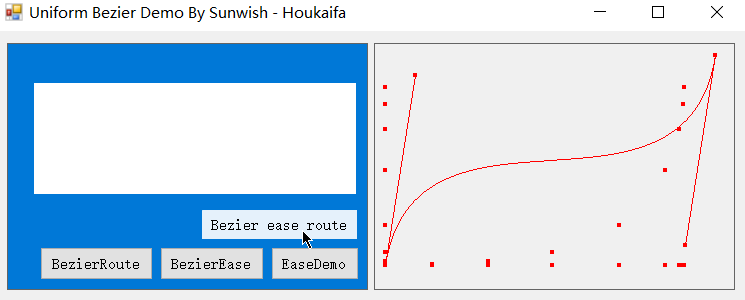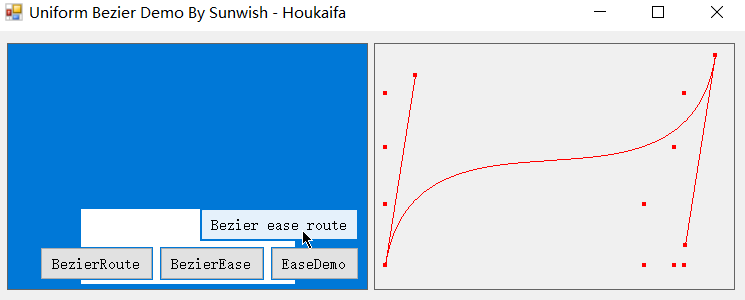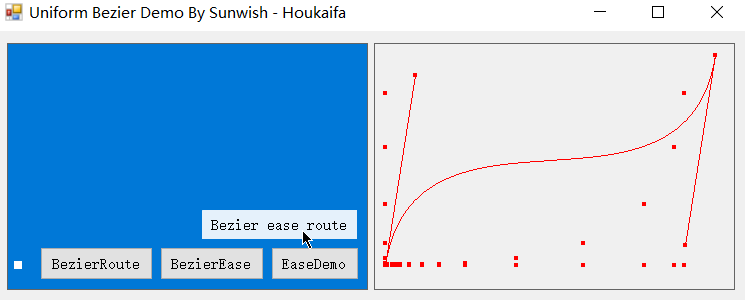
这篇文章其实算是填了之前那篇的坑,在之前《贝塞尔曲线运动n阶追踪方程的数学原理及其匀速化方法和应用》中有许多实现细节聊地相当模糊,实现和应用部分一笔带过,也没有区分两种匀速化,除去推导出了 n 阶通式之外算是写的相当失败了hhh,本文对贝塞尔曲线及其应用做了更加具体深入的展开和探究,其中缓动方面的匀速化在网上鲜有文章,但我觉得是大有用武之地的,至少目前是自家 Easecurve 项目的内核。本片应当与之前那篇合并起来,才能算是《贝塞尔曲线运动n阶追踪方程的数学原理及其匀速化方法和应用》的完全体。
点击查看隐藏内容
- 感谢你赐予我前进的力量

